【物理学】変分原理の不思議【δI＝0】
物理学の基礎方程式（ニュートンの運動方程式やシュレーディンガー方程式など）、変分原理で記載されていることは聞いたことがある方もいるかと思います。
ただ、変分原理とどういった原理なのかを知っているでしょうか？
その内容について今回は整理して説明してみようと思います。
１．光はどのように進むのか？
変分原理とは何かを話す前に、まず素朴な疑問として光の進む経路を考える。そのことを説明するには、一般にフェルマーの原理を用いて説明される。
フェルマーの原理とは以下のようん内容である。
上記で説明されている内容は、すなわち、光の経路は直線となることを言っている。
すなわち、
同媒質中の光の経路は直線となる
原理と言われて説明されればそれまでだが、光の進む経路が直線となるのは数学的に説明できないか、もう少し考えてみよう。その為にはフェルマーの原理にある「停留値」と言う概念を知る必要がある。
停留値の概念・・・ある経路長に対して少しずれた経路長との差が
２次のオーダーの微小量となって、０と近似できる。
いまいち言葉だけだとわかりにくいので、下図を用いて説明する。
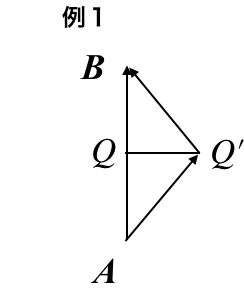
例１ではAを光源（始点）にA→Bへ光が進んだ時、直進する経路をAQB（l１）、直進しない経路AQ'B（l２）とする。この２経路のうち、結果どちらを選択して光は進むのかを考えることが目標である。その際に着目する内容は２つの経路のズレQQ’であり、この量を用いて２つの経路の差をΔlを表すとすれば、
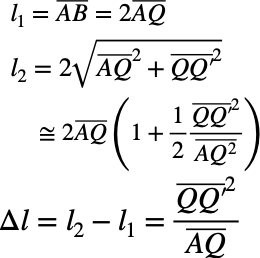
このQQ’が停留値として働く。すなわち、QQ’は２次オーダーを０とすれば、この場合、２つの経路に差がなく、AQBと進むので経路は直線となる。つまり、何らかの２つの量に関して２つの量のズレがあり、そのズレが２次のオーダーになっている場合を停留値をとるという。１次のオーダーの場合は０とみなせないので、この場合は停留値とみなさない。（例２）これにより、様々な経路を考えられる中、直線しか選ぶことができないと言っているのがフェルマー原理の主張である。この考え、停留値の概念が変分原理の出発点である。
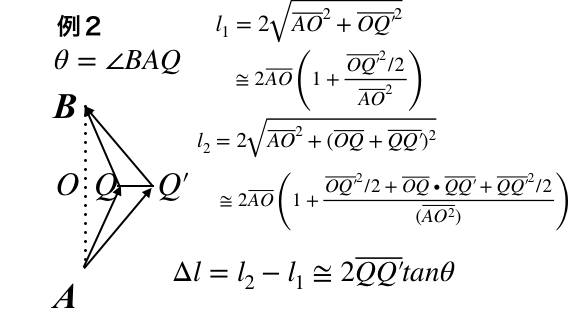
２．変分原理を解析的に
同じような考えを解析的に考えてみよう。その際に、停留値の概念を少し書き直す。
停留値の概念・・・ある経路長に対して少しずれた経路長との差が
２次のオーダーの微小量となって、０と近似できる。
停留値の概念・・・ある関数の経路長に対して少しずれた経路長との差が
２次のオーダーの微小量となって、０と近似できる。
数学の「関数」を付け加えただけである。よって、２つの関数のズレを評価して停留値をとるとはどのような数式で表すことができるのかを調べる。その為に以下の関数を定義する。
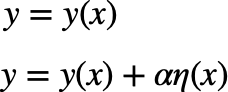
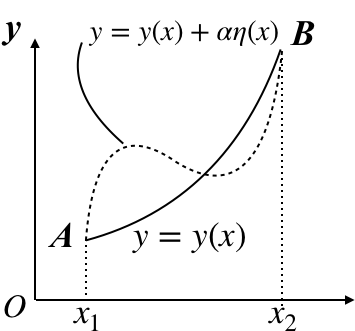
ηはxに依存するズレの関数である。αは適当な変数であるが、y（x）からのズレのオーダーを示し、xとは独立であることに注意してほしい。ここで、この関数の経路、曲線A Bが停留値をとる場合どのような経路を描くかを考える。曲線ABの線素をdsとすれば、経路長Iは
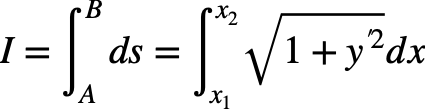
被積分関数をF(x, y, y'）とすれば、
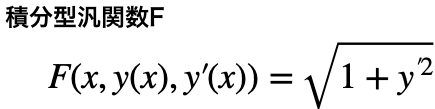
経路長Iはこの関数に依存するので、経路長Iが停留値をとる場合においてこの積分型汎関数Fに関する方程式を立てるのが目標となる。
さて、上記の経路長Iに関してy(x)をy(x)+αη(x)へ変更した場合、yもy’も、ηもxの関数なので、経路長はαに依存することとなる。
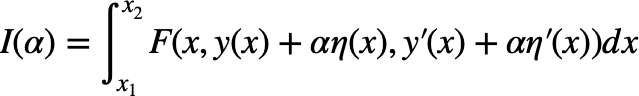
細かいことを言えば、y、y’、ηは［x_1, x_2］で連続かつ微分可能であることを前提としている。また、図から読み取れるようにη（x_1)=η(x_2)=0である。
さて、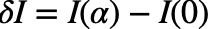
を考える。そして、停留値を考えるときので経路長Iの差分を取る。このとき、別関数のズレに対して評価する際には一般的にδを用いる。
αに対して2次のオーダーでテイラー展開を用いると、
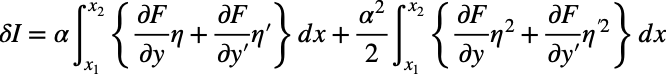
第２項は２次のオーダーなので、停留値の概念から０と近似できるが、第１項には１次のオーダが残っているので、あれ、何かがおかしいのかな？と思うかもしれない。これは特に問題なはない。ここでα＝０でδI＝0となるのは明確なので、I(α)はα＝０で極値をとるということ（Iの変化がない）。すなわち、δI = 0の時、その条件はα=0もしくは第１項の積分が０なので、I(α)が極値を持つのは当然α＝０だから、δI＝０の条件を満たすのならば、I (α)は極値を持つ。その為、テイラー展開して微分すればいい。
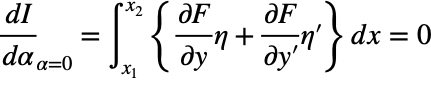
すなわち、δIの第１項の積分部分は既に０であるということなので、αに寄らず以下の通りとなる。（重要）
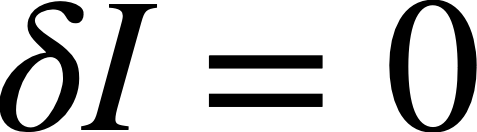
注意するのは、確かにα＝０でも同じ結果となるが、経路長Iが極値をとるということが重要であるということ。なので、以下の式が重要だということである。
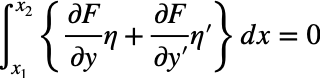
部分積分を用いて整理すると、
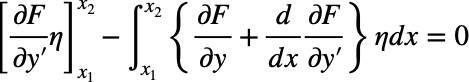
第１項はηにより０、第２項はηが任意の関数の為、{}内が０である必要がある。
したがって、その式には名前がついており、
この式が停留値を満たす基礎方程式となる。すなわち、変分原理とはこの方程式を満たすことを前提した原理ということである。
３. オイラー・ラグランジュの方程式の扱い方
前説で得られた方程式はFに関する偏微分方程式だが、その実はy(x)を求めるための方程式である。実際に、オイラー・ラグランジュの方程式を扱うときにはFの関数は既に知っており、その関数の変数扱いとなっているy(x)に対する微分方程式に書き直される。
さて、オイラ・ラグランジュの方程式は以下の通りだった。
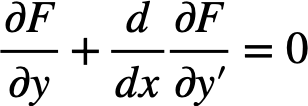
関数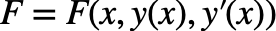 
であるが、解く問題によっては変数（関数）を含まない物をあるだろう。そのため、以下のパターンの場合のオイラー・ラグランジュの方程式を書き下す。
・汎関数 Fがyを陽に含まない
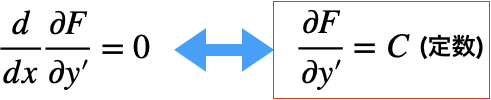
・汎関数Fがxを陽に含まない
・汎関数Fがy’を陽に含まない
※この場合は単なる曲線を表し、境界条件を満たさない。
導出はxを陽に含まない場合のみややこしいが、式を整理すると、赤枠のような綺麗な式変形が可能である。ちなみに、陽に含まないとは、汎関数内には変数として存在しないことをいう。つまり、xを陽に含まないとは、Fはy、y’の関数でxの関数ではないが、y、y’はxの関数であるよということを言っている。よって、この場合、単純にxで微分すると０というわけにいかないことに注意する必要がある。
全て含んでいる場合は、オイラー・ラグランジュの方程式を単純に解き進めればいいが、
○○を陽に含まない場合は上記の赤枠で示した式を用いると楽である。
４. オイラー・ラグランジュの方程式を使ってみる
１章で考えた光の進む経路の話をオイラー・ラグランジュの方程式を用いて考えてみよう。
AとBを結ぶ任意の曲線の長さは上図から線素dsとすれば、
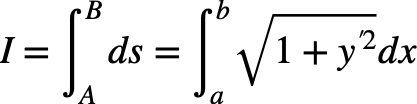
汎関数Fはというと、
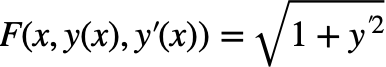
この場合はFはyを陽に含まないので、
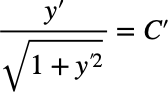
C'は任意の定数である。y'に対して整理すると、
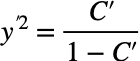
仮にy’>０とすれば、右辺を改めて定数Cとすると、求めるy (x)は右肩上がりの直線となる。（C＞０,Dも任意の定数）つまり、以下の式で書き表される。
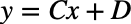
要するに、フェルマーの原理を数学的に記述するとしっかりと直線を示すことができる。この２点を結ぶ経路を変分原理として示す問題を最短距離問題という。これは曲線で結ぶよりも直線で結ぶ方が距離が短いという経験的も直感的にも当たり前のことを数学的に示しただけだが、この問題を力学的な問題に当てはめて考えるとなかなか経験的、直感的にもわかりにくいことを理解することができるようになる。その例が最速降下の問題である。
最速降下とは何か？をまず説明しよう。当然だが、空中で物を離すと物は落下する。重力に引っ張られるからということは一般的に知られている話で、物理の逸話としてもニュートンが万有引力の法則を発見したという話の中でも木からリンゴが落ちるのを見たからと説明されているくらいよく知られている話だろう。さて、ここで１つ疑問を投げかけよう。その落下する物を適当なレールや滑り台みたいな経路で進む場合には最短時間で滑り落ちるのはどのような経路を通ったときなのか？
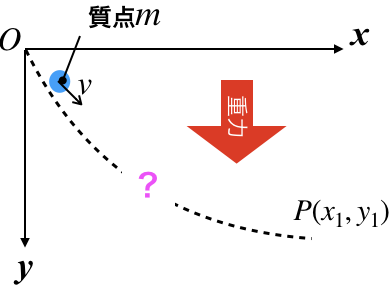
要するに、最速降下の問題とは。「重力が働く、摩擦なき経路に置いた物体（ここではわかりやすく質点）を考える。どのような経路（曲線）上であれば、最短時間で転がり落ちるか？」という問題である。この問題を考える上で重要なのは、エネルギーの保存である。質量m、速度vとすれば、
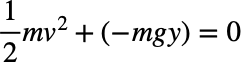
速度の２乗は各成分x、yの時間tで微分したに記載できるので、エネルギーの保存則をdtで整理すると、
すなわち、
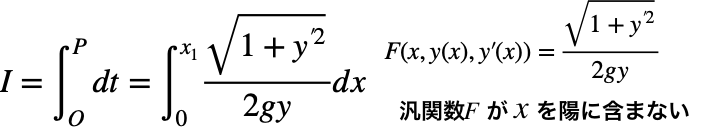
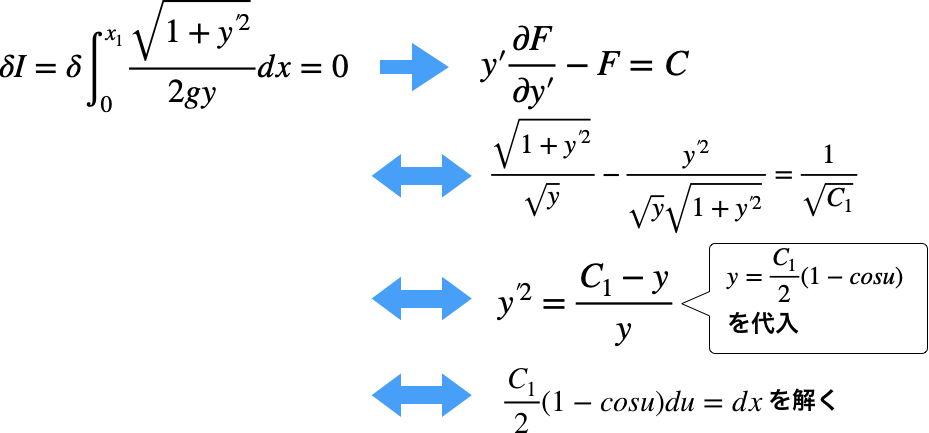
yは置換時に算出しており、xは媒介変数uの積分で求まる。これはサイクロイド曲線となる。
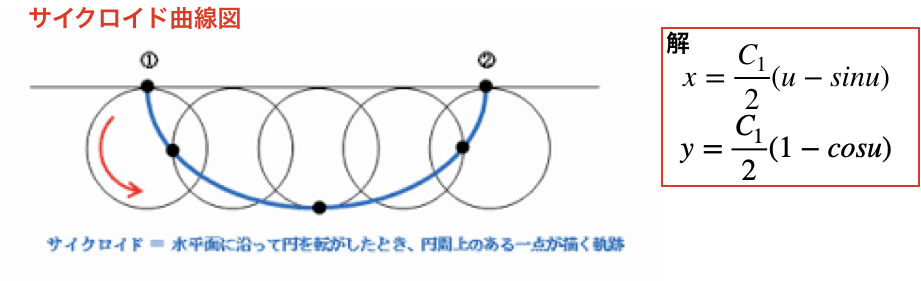
直感的には最短経路である直線ではないかと考えてしまう。このように重力のみが働いている場合ではあるが、変分原理（オイラー・ラグランジュの方程式を解くということ）を用いることで物を最速で降下させる曲線がサイクロイド曲線であると求める事ができる。
最短経路であれば、最短時間では到着するわけではない！！！
参考文献
物理数学One point 4 べんりな変分原理 岡本 誠著
